|
王冬計1,李營2,劉聯勝1,劉春雨2,賈思琪1,董奇烜1
(1.河北工業大學能源與環境工程學院,天津300401;2.河北工業大學經濟管理學院,天津300401)
摘要:采用秸稈壓塊燃料采暖是減少污染物排放的措施之一,秸稈壓塊服務站的建設是實施該采暖的基礎。基于博弈論對服務站建設進行分析,構建政府、企業、農民的動態博弈模型,分析博弈策略的穩定性。結果表明,政府激勵在三方決策中起著重要作用,其激勵策略受農民采用秸稈壓塊采暖所付出成本的影響。當其對企業和農民的補貼比例在40∶1時企業和農民均參與該項目。此外采用Shapley值法進行利潤分配,政府、企業、農民的利潤占比分別為9.06%、69.17%、21.77%。
北方農村地區燃煤采暖造成嚴重的環境污染,對居民身體健康產生嚴重威脅[1]。為營造舒適、清潔的居住環境,急需推廣清潔采暖方式。秸稈具有低灰、低硫、低氮、CO2零排放等優點[2-3],用秸稈壓塊燃料替代散煤取暖已成為解決能源問題和改善生態環境的有效途徑之一[4]。然而,傳統的秸稈直燃方式因存在燃料收集與使用勞動強度高、堆放占用空間大等問題,而被逐漸富裕起來的農民舍棄。采用成型技術將松散的秸稈(60~80kg/m3)壓縮為壓塊燃料(700~1300kg/m3)既便于運輸、存儲,又可以有效提高燃料的能量密度[5],使其便于使用,用于農村采暖不僅可以減少化石燃料消耗,還可減少溫室氣體排放,是一條可行的可持續發展道路[6-8]。
目前,中國的秸稈壓塊燃料供應鏈多呈“農戶→秸稈經紀人→壓塊生產企業→燃料市場”的模式。秸稈被農民低價出售給秸稈經紀人,經多級秸稈經紀人后由壓塊生產企業收購,成型后的產品在燃料市場出售。該供應鏈屬于單向多層的服務模式,成型燃料因多次利潤疊加而價格高昂,致使農民使用壓塊燃料的意愿較弱,形成了農民僅供應秸稈原料而不使用壓塊產品的開環結構,供需兩側的物質與價格均不穩定。造成該現象的主要原因是對農戶的行為模式認識不夠準確,將農戶行為模式認為是典型的經濟人。實質上,農民既是秸稈供應者又是壓塊燃料消費者。在農村地區構建秸稈壓塊服務站公共服務設施,形成“農戶→秸稈壓塊服務站→農戶”,則可去除供應鏈的中間環節,構建穩定可靠的區域能源市場體系,實現以可再生能源替代散煤供暖,進而達到節能減排的效果。
秸稈壓塊服務站在組織關系上涉及到當地政府、企業和農民三部分,三者不是孤立的個體而是互利共贏的合作者。研究三方參與主體的行為策略是一個典型的博弈問題,解決博弈問題一直存在很多方法,如靜態博弈、動態博弈、重復博弈等[9]。但以上博弈理論沿襲經典經濟學的完全理性人假設[10],即政府、企業和農民均被視為完全理性人,在一次博弈或重復博弈中即可找到最佳策略。然而這一假設與實際是不相符的。實際情況下各參與主體的知識、能力及智慧等方面是不同且有限的,而且僅僅通過簡單的重復博弈是不能使所有參與主體達到“共同知識”的[11]。秸稈壓塊服務站建設博弈過程,不僅涉及農民、企業及政府各主體客觀的經濟行為,還存在農民和企業可能不知道其他參與主體收益函數的情況,并且各主體都有各自的習慣和經驗,存在系統推理誤差等主觀因素。政府、企業及農民都是有限理性人,且三方之間的博弈是一個信息不完全的復雜動態博弈過程。演化博弈論認為人的理性是有限的,不要求完全信息條件,它強調一種動態均衡[12]。為此選取演化博弈理論對秸稈壓塊服務站建設問題進行研究。
首先構建政府、企業及農民三方博弈模型;其次,結合演化博弈穩定性理論尋找三方博弈的穩定點,討論不同條件下模型的穩定狀態,分析各參與主體的行為策略;然后采用Shapley值法建立利潤分配模型;最后結合案例對政府的激勵和三方利潤分配占比進行量化分析,以期為政府制定合理的激勵策略提供理論支持。
1演化博弈模型的構建
演化博弈理論包括復制動態方程[13]和演化穩定策略[14]兩方面內容。前者強調的是選擇,后者強調的是變異。復制動態方程是描述博弈方的某一特定策略在一個種群中被采用頻數的動態微分方程。演化穩定策略是指在多方博弈過程中,由于博弈方都是有限理性的,不可能在起初就找到各自最優策略,博弈方需對有利策略不斷修正和改進,直至趨于某個穩定策略。
1.1模型假設與參數
秸稈壓塊服務站的建設由政府、企業和農民三方群體組成。通過分析各群體行為,構建三方演繹博弈模型。在三方博弈中,政府以社會效益和環境效益最大化為決策依據;企業以自身利益最大化為決策依據;農民以自身受益最大化為決策依據。政府的決策為采取經濟激勵政策或不采取經濟激勵政策,企業的決策為投資建設秸稈壓塊服務站或不投資建設秸稈壓塊服務站,農民的決策為采用秸稈壓塊取暖或不采用秸稈壓塊取暖。基于上述參與主體的決策行為,做出如下假設。
假設1:政府、企業和農民之間的博弈屬于不完全信息博弈,即三方掌握的信息均不完全。
假設2:農民不采用秸稈壓塊取暖所帶來的環境損失,在政府采取經濟激勵政策、企業建設情況下,政府和企業共同承擔該項損失,其中政府承擔比例為β,企業承擔比例為1-β;其余情況下政府承擔該項損失。
各參與主體的相關參數設定如下:
政府采取經濟激勵政策需付出的成本記為C1,萬元;政府不采取經濟激勵政策需付出的宣傳成本記為C2,萬元。其他參與主體均積極參與下政府獲得的社會效益和環境效益記為R1,萬元;其中因企業的積極參與政府獲取的效益比例為θ;其他參與主體均不參與下政府的損失記為D1,萬元。
企業投資建設秸稈壓塊服務站付出成本記為C3,萬元;獲得的經濟效益記為R2,萬元;獲得的政府補貼記為W1,萬元。企業不建設秸稈壓塊服務站損失的社會聲譽記為C4,萬元。
農民采用秸稈壓塊取暖需付出燃料成本記為C5,萬元;獲得的政府補貼記為W2,萬元。農民不采用秸稈壓塊取暖需付出燃料成本記為C6,萬元;造成的環境損失記為D2,萬元。
1.2模型建立
根據以上假設,構建圖1所示的政府G、企業E和農民F之間的博弈樹模型。圖中yes代表主體的行為是參與秸稈壓塊服務站的建設和使用,no代表主體的行為是不參與秸稈壓塊服務站的建設和使用。數字1、2、3、4、5、6、7、8分別代表不同的情況,如數字1表示政府采取經濟激勵政策、企業投資建設秸稈成型燃料服務站、農民采用秸稈壓塊取暖的情況。

根據上述博弈樹模型得出農民采用秸稈壓塊取暖與不采用秸稈壓塊取暖的收益情況分別如表1、表2所示。

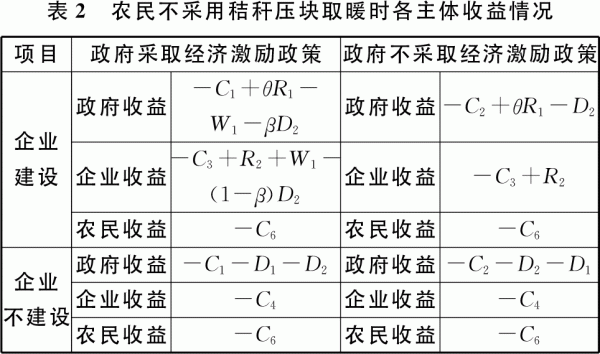
1.2.1政府的博弈策略
設定政府采取經濟激勵政策的概率為x,則政府不采取經濟激勵政策的概率為1-x;企業投資建設秸稈壓塊燃料服務站的概率為y,則企業選擇不投資建設秸稈壓塊燃料服務站的概率為1-y;農民采用秸稈壓塊取暖的概率為z,則農民不采用秸稈壓塊取暖的概率為1-z。政府、企業、農民的平均期望收益分別用H1、H2、H3表示。

隨著群體不斷演化,群體中的個體不斷選擇某策略進行博弈,采用某策略的個體的期望收益高于群體平均收益,則該類個體的數量會增加;反之,則該類個體的數量會減少。這就表明在演化過程中群體中個體總數量一直處于不斷變化中,而采取經濟激勵政策策略的個體概率也在不斷變化,用于描述這個概率變化情況的方程即為復制動態方程。采用復制動態方程,即選擇某一特定策略概率的變化等于該策略的收益值與群體平均收益值之間的差值[14-15]。基于此,政府采取經濟激勵政策策略的復制動態方程x′(t)由式(4)進行計算,即


1.3三方演化路徑及穩定性分析
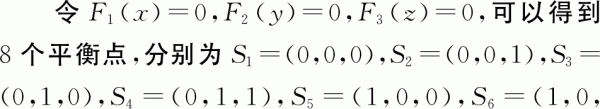

1.3.1政府的演化穩定策略
1)當yz(β-1)D2-y[(1-β)D2-W1]-zW2-C1+C2=0,即y、z取式(17)中的數值時,表明x取任意值,系統都處于穩定狀態,不再演化。此時政府既可以選擇采取經濟激勵政策,也可以選擇不采取經濟激勵政策。
2)當yz(β-1)D2-y[(1-β)D2-W1]-zW2-C1+C2<0時,dF1(0)/dx<0,dF1(1)/dx>0。依據微分方程穩定性判別條件,當F′(x)≤0時取得穩定,則可得x=0為演化穩定策略。表明政府逐漸從采取經濟激勵政策的策略向不采取經濟激勵政策的策略演化,即不采取經濟激勵政策是此時政府的演化穩定策略。
3)當yz(β-1)D2-y[(1-β)D2-W1]-zW2-C1+C2>0時,dF1(0)/dx>0,dF1(1)/dx<0。此時x=1為演化穩定策略,表明政府逐漸從不采取經濟激勵政策的策略向采取經濟激勵政策的策略演化,即采取經濟激勵政策是此時政府的演化穩定策略。
1.3.2企業的演化穩定策略
1)當x[W1-(1-β)D2]+xz(1-β)D2-C3+R2-C4=0,即x,z取式(17)中的數值時,表明y取任意值,系統都處于穩定狀態,不再演化。此時企業既可以選擇投資建設秸稈壓塊服務站,也可以選擇不投資建設秸稈壓塊服務站。
2)當x[W1-(1-β)D2]+xz(1-β)D2-C3+R2-C4<0時,dF2(0)/dy<0,dF2(1)/dy>0。此時y=0為演化穩定策略,表明企業逐漸從投資建設秸稈壓塊服務站的策略向不投資建設秸稈壓塊服務站的策略演化,即不投資建設秸稈成型燃料服務站是此時企業的演化穩定策略。
3)當x[W1-(1-β)D2]+xz(1-β)D2-C3+R2-C4>0時,dF2(0)/dy>0,dF2(1)/dy<0。此時y=1為演化穩定策略,表明企業逐漸從不投資建設秸稈壓塊服務站的策略向投資建設秸稈壓塊服務站的策略演化,即投資建設秸稈壓塊服務站是此時企業的演化穩定策略。
1.3.3農民的演化穩定策略
1)當xW2-C5+C6=0,即x取式(17)中的數值時,表明z取任意值,系統都處于穩定狀態,不再演化。此時農民既可以選擇采用秸稈壓塊取暖,也可以選擇不采用秸稈壓塊取暖。
2)當xW2-C5+C6<0時,dF3(0)/dz<0,dF3(1)/dz>0。此時z=0為演化穩定策略,表明農民逐漸從采用秸稈壓塊取暖的策略向不采用秸稈壓塊取暖的策略演化,即不采用秸稈壓塊取暖是此時農民的演化穩定策略。
3)當xW2-C5+C6>0時,dF3(0)/dz>0,13基于演化博弈論的秸稈壓塊服務站建設分析及利潤分配dF3(1)/dz<0。此時z=1為演化穩定策略,表明農民逐漸從不采用秸稈壓塊取暖的策略向采用秸稈壓塊取暖的策略演化,即采用秸稈壓塊取暖是此時農民的演化穩定策略。
1.4三方共同作用的演化策略穩定性分析
根據Ritzberger和Weibull[16]提出的結論,只需對S1=(0,0,0),S2=(0,0,1),S3=(0,1,0),S4=(0,1,1),S5=(1,0,0),S6=(1,0,1),S7=(1,1,0),S8=(1,1,1)8個均衡點的穩定性進行分析。有學者提出應用雅可比矩陣的局部穩定性可得到均衡點的穩定性[17]。根據博弈三方的復制動態方程,可以得到如表3所示的雅可比矩陣。
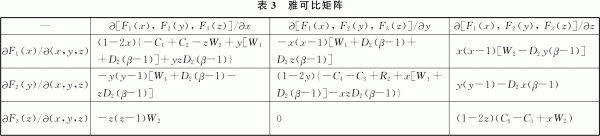
由李亞普諾夫第一法則可知,演化穩定策略(ESS)對應的雅可比矩陣的特征根必須小于0[18]。各均衡點的特征根值如表4所示。

即當政府、企業及農民的付出成本和收益大小符合上述條件時,政府采取經濟激勵政策策略、企業采取建設策略、農民采取采用秸稈壓塊取暖策略的概率均為1。
2模型分析
2.1政府行為分析
依據式(17)可得政府采取經濟激勵政策的概率為x=(C5-C6)/W2。政府的策略選擇取決于農民采用秸稈壓塊取暖需付出的燃料成本C5、農民不采用秸稈壓塊取暖需付出的燃料成本C6及政府給予農民的補貼W2。與農民采用秸稈壓塊取暖需付出的燃料成本C5成正比,與農民不采用秸稈壓塊取暖需付出的燃料成本C6和政府給予農民的政府補貼W2成反比。這表明農民采用秸稈壓塊取暖的成本越高,政府越需要加大經濟激勵力度,以提高農民的參與積極性。農民不采用秸稈壓塊取暖的成本越高,政府的經濟激勵力度可以相應減弱。
2.2企業行為分析


2.3農民行為分析
農民選擇采用秸稈壓塊取暖的概率為z={W2(C3+C4-R2)-(C5-C6)[W1-(1-β)D2)]}/[(1-β)D2(C5-C6)]。當政府補貼W2=[(C5-C6)W1]/(C3+C4-R2)時,農民選擇采用秸稈壓塊取暖的概率為1。通過政府補貼W2的表達式可看出政府對農民的補貼力度與農民采用秸稈壓塊取暖需付出的燃料成本C5成正比,與農民不采用秸稈壓塊取暖需付出的燃料成本C6成反比。這表明當采用秸稈壓塊取暖成本過高時,為了提高農民采用的積極性,政府需要加大對農民的補貼力度;當農民不采用秸稈壓塊取暖,仍采用燃煤取暖的成本越小時,農民對燃煤取暖的認可度越高,相應也就需要政府加大對農民采用秸稈壓塊取暖的補貼力度以促使農民放棄燃煤取暖。因此,政府可以通過限制煤炭使用量、調整煤炭價格、對超額燃燒煤炭的農民收取一定比例的懲罰費用等措施來提高農民燃煤成本,從而提高農民采用秸稈壓塊取暖的積極性。
3利潤分配
根據博弈局中人之間是否具有約束力的協議,可以將一個博弈過程分為合作博弈和非合作博弈。合作博弈主要研究在博弈局中人之間具有約束力的協議并使得整體利益最大時,各局中人如何分配收益的問題。其中,合作是合作博弈的基礎,團體理性是其重點。根據前文政府、企業、農民三者之間的博弈模型,假設三者達成合作協議,進行合作博弈模型建立,得出三者的合理利益分配。
Shapley值法由Shapley于1953年提出,為解決多個局中人在合作過程中因利益分配而產生矛盾的問題,屬于合作博弈領域。該方法是按照成員對聯盟的邊際貢獻率將利益進行分配,即成員i所分得的利益等于該成員為其所參與聯盟創造的邊際利益的平均值。基于Shapley值進行聯盟成員的利益分配避免了分配上的平均主義,比任何一種僅按資源投入價值、資源配置效率及將二者相結合的分配方式都更具合理性和公平性,也體現了各盟員相互博弈的過程[18-19]。因此,采用Shapley值法對政府、企業、農民博弈進行利潤分配。
3.1 Shapley值法概述


3.2秸稈壓塊服務站合作的利益分配模型
3.2.1構建利潤分配模型
秸稈壓塊服務站的合作博弈模型中有3個局中人:政府、企業和農民,分別記為A、B、C,局中人的策略都是要么合作要么不合作。現考慮的是合作博弈,3個局中人在博弈前都簽訂協議,合作形成一個聯盟,根據上述介紹的Shapley值法可以計算大聯盟中每個局中人的利益。下面首先計算各聯盟的利益情況。
1)當3個局中人相互獨立,即Shapley值法中的S=1時,各博弈局中人的利益情況如下:
政府(A)單獨采取經濟激勵政策獲得收益為v(A)=(-C1-D1-D2)。
企業(B)單獨選擇建設服務站獲得收益為v(B)=(-C3+R2)。
農民(C)單獨選擇采用秸稈壓塊取暖獲得收益為v(C)=(-C5)。
2)當3個局中人兩兩合作,即Sharpley值法中的S=2時,各聯盟的利益情況如下:
當政府(A)與企業(B)合作時,相當于政府采取經濟激勵政策,企業選擇建設服務站,農民選擇不采用秸稈壓塊取暖,此時兩者形成聯盟的利益為v(A,B)=(θR1+R2-D2-C1-C3)。
當政府(A)與農民(C)合作時,相當于政府采取經濟激勵政策,企業選擇不建設服務站,農民選擇采用秸稈壓塊取暖,此時兩者形成聯盟的利益為v(A,C)=(-C1-D1-C5)。
當企業(B)與農民(C)合作時,相當于政府不采取經濟激勵政策,企業選擇建設服務站,農民選擇采用秸稈壓塊取暖,此時兩者形成聯盟的利益為v(B,C)=(-C3+R2-C5)。
3)當3個局中人都參與合作形成大聯盟,即Sharpley值法中的S=3時,聯盟的利益情況如下:
當政府(A)、企業(B)與農民(C)均合作時,相當于政府采取經濟激勵政策,企業選擇建設服務站,農民選擇采用秸稈壓塊取暖,此時三者形成聯盟的利益為v(A,B,C)=(R1+R2-C1-C3-C5)。
3.2.2模型求解
根據式(20)以及各聯盟的利益情況,可以計算聯盟中各局中人的邊際貢獻。該合作博弈中共有3個局中人,聯盟S中的人數依次取1、2、3,分別對應各局中人相互獨立、兩兩合作以及形成統一大聯盟時的利益情況。下面求解各局中人的邊際貢獻。
3.2.2.1政府獲利情況
政府(A)可以組成的聯盟有4種情況:{A}、{A,B}、{A,C}、{A,B,C}。依據Shapley公式計算得到政府(A)各聯盟概率值、利益情況及總利潤情況,如表5所示。

依據表5可得:政府(A)單獨參與項目的概率為1/3,此時政府獲利-C1-D1-D2;政府分別與企業、農民合作參與服務站建設項目的概率均為1/6,此時政府獲利分別為θR1-D2-C1、-C1-D1;政府、企業、農民三方合作參與的概率為1/3,此時政府獲利為R1-C1。
綜上,政府總獲利xA(v)=1/6[(θ+2)R1-6C1-3D1-3D2]。
3.2.2.2企業獲利情況
企業(B)可以組成的聯盟有4種情況:{B}、{A,B},{B,C},{A,B,C}。依據Shapley公式計算得到企業(B)各聯盟概率值、利益情況及總利潤情況,如表6所示。

依據表6可得:企業(B)單獨參與項目的概率為1/3,此時企業獲利(-C3+R2);企業分別與政府、農民合作參與服務站建設項目的概率均為1/6,此時企業獲利分別為θR1+R2+D1-C3、-C3+R2;企業、政府、農民三方合作參與的概率為1/3,此時企業獲利為R1+R2+D1-C3。
綜上,企業總獲利xB(v)=1/6[6R2+(θ+2)R1+3D1-6C3]。
3.2.2.3農民獲利情況
農民(C)可以組成的聯盟有4種情況:{C}、{A,C}、{B,C}、{A,B,C}。依據Shapley公式計算得到農民(C)各聯盟概率值、利益情況及總利潤情況,如表7所示。

依據表7可得:農民(C)單獨參與項目的概率為1/3,此時農民獲利-C5;農民分別與政府、企業合作參與服務站建設項目的概率均為1/6,此時農民獲利分別為D2-C5、-C5;農民、企業、政府三方合作參與的概率為1/3,此時農民獲利為(1-θ)R1+D2-C5。
綜上,農民總獲利xC(v)=1/6[2(1-θ)R1+3D2-6C5]。
3.2.2.4利潤分配比例
得到3個局中人的邊際貢獻后,將其單位化即可得到每個局中人在大聯盟中的利益分配比例。令xT(v)=xA(v)+xB(v)+xC(v),則政府(A)應得的利益分配比例為xA(v)/xT(v),企業(B)應得的利益分配比例為xB(v)/xT(v),農民(C)應得的利益分配比例為xC(v)/xT(v)。
根據各局中人的Shapley值,可以得到各局中人的利益分配比例如下。
政府的利潤分配比例wA由式(21)進行計算,即

4案例
某企業計劃投資建設秸稈成型燃料服務站,計劃投入成本100萬(建廠費50萬,設備費30萬,人工20萬)。設定政府補貼期限為5年。由于該企業為工程建設企業,依據非居民所得稅核定征收管理辦法中第五條規定,從事承包工程作業、設計和咨詢服務的成本利潤率為15%~30%。假定該企業每年預計利潤率為25%,即企業每年利潤為25萬,5年總利潤額為125萬元。企業不投資建設秸稈壓塊服務站,5年損失的社會聲譽總共為5萬元。農民若采用燃煤取暖,每年需要煤2t,每噸800元,即年成本為0.16萬元,5年總成本為0.8萬元;若采用秸稈壓塊取暖,每年需要4t,每噸150元,即年成本為0.06萬元,5年總成本為0.3萬元。農民不采用秸稈壓塊取暖每年所帶來的環境損失為6萬元,5年總成本為30萬元,其中政府承擔損失比例為2/3。政府年宣傳成本為7萬,5年總成本為35萬元。政府推行經濟激勵政策付出的年成本為5萬,5年總成本為25萬元。政府獲得的年社會效益和環境效益為企業收益的1.4倍,即政府的5年總收益為175萬元,其中因企業的積極響應政府獲取的效益比例為3/5。企業和農民均不參與項目下政府的年損失為8萬元,5年的總成本為40萬元。企業和農民均不參與時政府沒有補貼支出。
依據企業和農民參與概率均為1時的政府補貼表達式,將上述數據代入計算得知,政府每年需補貼企業8.7295萬元,每年需補貼農民0.2182萬元,5年內政府補貼開支為44.7385萬元。同時,在秸稈壓塊服務站建設和運行過程中,企業和農民始終是利益相關者,雙方的策略選擇都受到政府政策的影響,同時農民的參與程度也會影響企業投資建設秸稈壓塊服務站的積極性。對于政府而言,其對雙方的補貼比例應該控制在一定范圍內,這樣既可以提高雙方參與積極性,又可以節省財務開支。若政府對雙方的補貼比例失衡,一方面這可能會降低某一方的參與積極性,另一方面也會增加政府財政支出。因此,確定一個相對合理的補貼比例對秸稈成型燃料服務站的建設和運行起著至關重要的作用。確定政府對企業和農民的補貼比例范圍在40∶1時雙方參與積極性最高。
依據式(21)~式(23),將上述數據代入計算得知,政府的利益分配占比為9.06%,企業的利益分配占比為69.17%,農民的利益分配占比為21.77%。
5結論
通過構建政府、企業以及農民三方參與主體的演化博弈模型,分析了不同情況下三方參與主體的演化結果,并對三方參與主體的行為進行了分析,得出以下主要結論:
1)政府采取經濟激勵政策策略的概率受農民采用秸稈壓塊取暖需付出的燃料成本以及不采用秸稈壓塊取暖需付出的燃料成本的影響。與農民采用秸稈壓塊取暖需付出的燃料成本成正比關系,與農民不采用秸稈壓塊取暖需付出的燃料成本成反比關系。兩種采暖方式的成本差距越大,政府越傾向于采取經濟激勵政策。
2)企業采取建設策略的概率取決于政府滿足企業自身補貼需求的程度。當政府出臺相關財政補貼政策完全滿足企業補貼需求后,企業選擇參與建設秸稈壓塊服務站的概率為1。同時研究表明,政府對企業的補貼力度與企業建設秸稈壓塊服務站需付出的建設成本成正比關系,與企業建設所得的經濟效益以及企業不建設損失的社會聲譽成反比關系。隨著企業建設成本降低或不建設損失成本升高,其對政府補貼力度的要求也會相應降低。
3)農民采取用秸稈壓塊取暖策略的概率取決于政府滿足農民自身補貼需求的程度。當政府出臺相關財政補貼政策完全滿足農民補貼需求后,農民選擇采用秸稈壓塊取暖的概率為1。同時研究表明,政府對農民的補貼力度與農民采用秸稈壓塊取暖需付出的燃料成本成正比關系,與農民不采用秸稈壓塊取暖需付出的燃料成本成反比關系。隨著農民采用秸稈壓塊取暖燃料成本的降低或農民不采用秸稈壓塊取暖燃料成本的升高,其對政府補貼力度的要求也會相應降低。
4)除政府補貼力度會影響企業和農民參與程度外,政府對企業和農民的補貼比例也影響著雙方策略選擇。一個合理的補貼比例在企業和農民均選擇參與該項目中發揮著至關重要的作用。企業和農民作為項目實施的利益相關者,雙方策略的選擇會相互影響。政府補貼比例不合理會導致某一參與主體積極性降低,從而影響另一參與主體的策略選擇。研究結果表明,當政府對企業和農民的補貼比例保持在40∶1時企業和農民均傾向于參與該項目。
5)在秸稈壓塊服務站建設運行項目中,政府從中分配的利潤最少,其次是農民,企業分配利潤最多。政府、企業、農民的利潤分配占比分別為9.06%、69.17%、21.77%,該結論與實際相符。政府作為宏觀調控機構,本身的關注點不在盈利,其主要承擔的是社會責任。而企業恰恰相反,其作為營利機構關注的焦點為利潤額。

 |
