|
趙宇,嚴永林
(中南林業科技大學,湖南長沙410000)
摘要:針對生物質粉料氣力輸送能耗高的問題,建立輸送管內兩相流數學模型。使用Fluent軟件仿真,分析顆粒在不同風速下水平輸送管道和豎直輸送管道內的受力和運動軌跡。為生物質粉料的輸送管道設計提供重要依據。
近年來,能源危機、空氣污染等問題逐漸受到世界各國的重視。生物質能源因具有清潔、易獲取、容易運輸和儲存、熱效率較高等特點受到廣泛的關注。從生物質原料至成品顆粒要經過原材料粉碎、干燥、壓模成型等幾個工序。目前一般采用氣力運輸完成原料粉碎后的輸送及干燥。分析輸送管道內粉料顆粒和氣體兩相流運動規律,對保證管道良好的輸送性能,防止管內結垢堵塞,降低能耗具有重要的作用。
目前國內關于氣力輸送的研究較多,例如:許盼等通過研究水平管道和豎直管道內的壓降情況得出豎直管道內固相的摩擦系數大于水平管道[1];王思佳等對生物質粉料的氣力輸送試驗研究,得出固氣比與輸送壓差的關系[2];李晟等通過氣固兩相流理論和多元回歸方法,得到在不同總壓降、載氣風量和流化風量下質量流量的計算公式[3]。但生物質顆粒在管道內的運動軌跡的研究文獻較少。本文通過數值模擬分析氣力輸送管道內顆粒的運動軌跡、受力情況及顆粒分布,為管道設計提供重要依據。
1數值分析和模型
1.1粉料顆粒物理性質
本文取木質粉料作為研究對象,通常含水量為10%~15%。根據文獻[3],顆粒物理性質如表1所示:
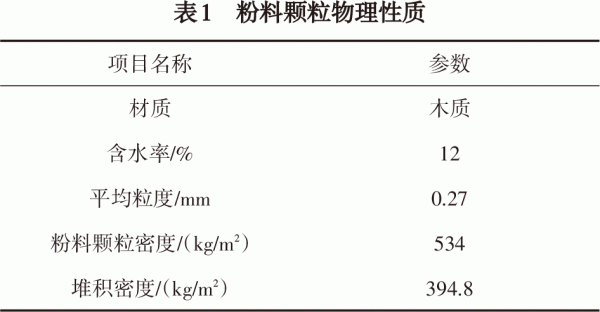
1.2數值分析
1)計算固相體積分數
固相的體積分數是研究兩相流重要參數之一。固相體積分數計算公式為:

文獻[1]中氣體流速在7m/s時,載荷量最大,為30kg/m2。結合公式(1)及表1計算得η=0.07,即生物質粉料在管道輸送中的最大體積分數為7%。因此本文的模型可以忽略固相顆粒間的相互碰撞和顆粒對氣體流場的影響。
2)構建數學模型模型

3)粉料顆粒運動控制方程
顆粒在氣體內受到慣性力、曳力、附加質量力、壓力梯度力、Basset力、重力、浮力、Magnus力、馬塞特力、Saffman升力,它們對顆粒的合力為0N。則顆粒運動控制方程可表示為:


對顆粒的受力做以下分析。選取重力作為參考,重力比浮力大兩個數量級,可忽略浮力影響。本文假設顆粒為光滑的球形,直徑為顆粒粒度,所受外力矩為0N·m,故忽略Magnus力。根據文獻[5]忽略Basset力。本文氣體為低流速氣體,顆粒與氣流的相對加速度較小,空氣密度低于粉料顆粒小兩個數量級,可忽略附加質量力。盡管目前還沒有雷諾數大于1的Saffman升力表達式,但根據它的定義同時參考式(11)可知,流場速度梯度越大,Saffman升力越大。由式(13)可知,壓力梯度力與流體壓力梯度相關,流場壓力梯度越大,壓力梯度力越大。由式(7)、(8)、(14)可知,顆粒受到的重力、曳力、慣性力與顆粒本身的性質和運動狀態有關。
4)粉料顆粒在豎直管道內臨界風速計算
粉料顆粒在輸送管道內的運動狀態可以分為懸浮流、底密流、疏密流、停滯流、部分流、柱塞流[6-8]。懸浮流、底密流、疏密流均屬于懸浮狀態輸送,輸送條件好的情況下不會對輸送管道造成堵塞。其中疏密流要求的風速最低,這種保持粉料顆粒懸浮的風速稱為臨界風速。
目前關于豎直管道內的臨界風速計算公式已經達到70多種。目前工程上常用的計算公式有:M.李伐公式、O.M托杰斯關系式、李森科提出的圖解法、羅曼科夫提出的通用關聯公式、普拉諾夫斯基提出的通用公式。本文選取普拉諾夫斯基通用公式計算在豎直向上管道內使顆粒懸浮的臨界風速,以此為基點展開討論。
將本文表1所示顆粒性質,并取氣溫20℃,標準氣壓下的空氣動力黏度17.8×10-6Pa·s,密度1.2kg/m3等數值代入普拉諾夫斯基通用公式計算。

1.3建立幾何模型
管道模型如圖1所示。為了讓粉料顆粒與氣流發展充分,適當的延長豎直管道和水平管道的長度。采用四面體非結構網格劃分,該網格適用于離散曲面等任何復雜的幾何形狀,網格劃分如圖2所示。
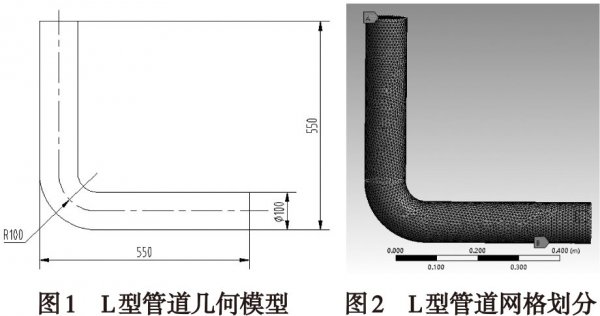
1.4計算方法與初始條件
商業軟件FLUENT中DPM模型適用于模擬離散相體積分數小于10%的顆粒運動。該模型遵循Euler-Lagrange法,將流體相視為連續體,使用拉格朗日法追蹤顆粒運動。
木質粉料顆粒的性質取表1所示參數,為簡化模型假設如下:1)粉料顆粒為理想球形;2)外界大氣壓101325Pa;3)氣流馬赫數低于0.3,假設氣體不可壓縮;4)忽略溫度變化對流場的耦合影響;5)粉料顆粒在入口均勻分布,與氣體流速相同;6)重力加速度9.8m/s2,豎直向下。其他初始條件和邊界條件設置為表2所示:

1.5模擬結果及分析
首先根據上文豎直管道內的臨界風速,模擬與重力反向的輸入氣體的顆粒軌跡,速度大小為1m/s。顆粒軌跡的模擬結果如圖3所示:
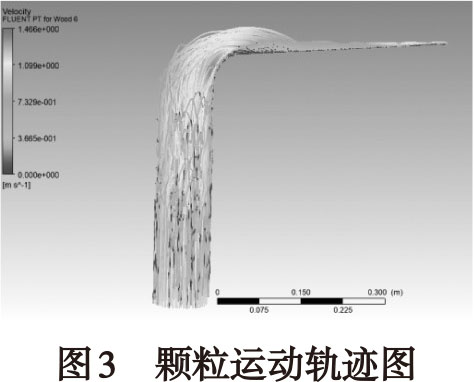
由圖3模擬結果可知,顆粒在豎直管道內處于懸浮狀態,符合上文臨界速度的計算。但由于風速過小導致水平管道內顆粒沉降至管底。
改變輸入速度分別為1m/s、2m/s、3m/s、4m/s、8m/s,豎直向下。顆粒軌跡模擬結果如圖4所示。
選取具有代表性的輸入速度為2m/s和8m/s的氣體速度矢量圖,如圖5所示。

由圖3可知,在1m/s的較低風速下,實現了豎直管內顆粒的流態化,這與臨界風速的計算結果相符。但顆粒速度較小,近壁面顆粒回落。顆粒輸送至水平管道后有拋射,隨后顆粒落入水平管道并不再揚起。該風速不符合氣力輸送要求。
由圖5(a~b)可知,豎直管道內的氣流速度在近壁面較小,速度梯度較大,而遠壁面局部范圍內氣流流速均勻。彎管及水平管道內,速度變化值幅度不大,結合本文粉料顆粒粒徑為0.27mm,顆粒兩側的氣流速度差不會很大,因此可忽略Saffman升力。由圖6(a~b)可知,流場內壓力梯度基本和速度梯度相同,忽略壓力梯度力對顆粒的影響。
首先分析各輸入速度下豎直管道內的顆粒軌跡、速度矢量、壓力。由圖4(a~e)可知,軌跡平行度較高,顆粒濃度分布均勻。顆粒速度輸入管道后加速,同時越靠近管中心速度越大。在豎直管道內,懸浮顆粒主要受重力和曳力的影響,重力大于曳力,曳力表現為阻力。周圍壁面的摩擦對顆粒的運動影響很大。
由圖4(a~e)可知,在彎管處所有顆粒以一定的速度撞擊彎管壁面,撞擊前后的小段區域軌跡折射角等于入射角,在彎管后半截上空形成“軌跡真空區域”。由于撞擊導致的動能損耗,使撞擊后顆粒速度低于氣體流速,顆粒對氣流表現出較差的追隨性。
顆粒經過彎管碰撞后有“揚起”的過程,初始輸入速度越大,揚起角度越大,即顆粒揚起越快。在本模型中的豎直管道內各顆粒軌跡線平行,如果忽略氣體“阻力”,入射角應等于折射角,即各圖的軌跡線的揚起角應相同。造成揚起角度不同的原因是碰撞過程中的顆粒動能損失:初速度越大動能損失越多,顆粒與流體的速度差越大,曳力的作用越明顯,揚起角越大。
顆粒在水平管后半段運動軌跡及分布分析:
1)當輸入速度為1m/s時,顆粒揚起隨后落下,落下后沒有再揚起,顆粒失去被氣流懸浮的能力,部分顆粒在管底的速度為0m/s,該特征表現為停滯流。在實際應用中,顆粒的群體運動為停滯—聚集—吹走的沙丘式移動,極易堵塞管道。
2)當輸入速度為2m/s時,顆粒獲得了懸浮能力,但顆粒揚起角度較小,穩定后軌跡上下疏密不均,軌跡高度小于管徑。在水平管道后段,顆粒軌跡有下降的趨勢。這是由于氣體懸浮力不足以抵消顆粒所受重力,部分顆粒停留在管道底部滑動。以上特征表現為疏密流,該風速是使顆粒在水平管道流態化的臨界風速。在實際應用中,顆粒在管道內的表現為碰撞—懸浮。由于與管壁碰撞時間極短,顆粒大部分時間仍處于懸浮狀態。在管道內壁質量理想,是最省能的輸送方式。
3)輸入速度增大至3m/s時,顆粒揚起角度增大,圖4(c)揚起角明顯大于圖4(b)揚起角。越靠近管底,顆粒分布越密,該特征表現為底密流。
4)輸入速度為4m/s、8m/s時,比較它們的軌跡圖,圖4(d)和圖4(e),揚起角度變化不明顯,水平管道內的軌跡線基本相同,該特征表現為懸浮流。懸浮流顆粒分布好,但要求的風速較高,能耗較高,管道磨損較大。
2結論
1)在管道內懸浮生物質粉料顆粒主要受重力、慣性力、曳力。
2)粉料在豎直管道內需要的流態化風速低于水平管道內的流態化風速,設計管道時可不考慮風速對豎直管道輸送性能的影響。
3)為保證輸送性能,降低輸送能耗,在保持一定的風速下應降低粉料顆粒的粒徑。同時較低風速下管道底部顆粒分布密集,應盡量保證管道內壁光滑。
參考文獻:
[1]許盼,陳曉平,梁才,等.生物質高壓密相輸送特性試驗研究[J].工程熱物理學報,2012,33(5):801-804.
[2]王思佳,靳世平,黃芬霞,等.生物質粉末氣力輸送特性試驗研究[J].工業加熱,2016,45(6):45-48.
[3]李晟,靳世平,舒朝暉,等.生物質粉料的氣力輸送能力實驗研究[J].工業鍋爐,2017(1):7-11.
[4]徐進,葛滿初.氣固兩相流動的數值計算[J].工程熱物理學報,1998,19(2):233-236.
[5]岑可法,樊建人.工程氣固多相流動的理論和計算[M].杭州:浙江大學出版社,1990.
[6]朱紅鈞,林元華,謝龍漢.Fluent12流體分析及工程仿真[M].北京:清華大學出版社:2011.
[7]馬勝,郭曉鐳,龔欣,等.粉煤密相氣力輸送流型[J].化工學報,2010,61(6):1415-1422.
[8]Jaworski Artur J,Dyakowski Tomaz. Investigations of flow instabilities within the dense pneumatic conveying system[J]. Powder Technology,2002,125(2):279-291. |
